Three for the Money: The Degree/Diameter Problem

Description

Materials

Instructions

Ideas for discussion

Materials

• One large copy of the puzzle graph that all students can see, such as one that is drawn on the floor with masking tape, or a copy for each student or group of students.
• Paper and pencil should be handy so students can experiment and draw their own solutions to the problem.

Instructions

1. Explain to students that you are going to tell them about a problem in mathematics that is easy to understand that no one has solved yet. There is no reason why one of them could not be the person to solve it.

   A famous mathematician, Paul Erdos, has offered a large cash prize for the person who succeeds in drawing the graph that solves this problem. They could win it.

2. Have the students look at the puzzle graph carefully. If they have played the games with Gertrude, Superperson and the Monster, they have already learned a lot about the structure of this graph. Explain that it has four properties or characteristics that mathematicians have found interesting:
   • Its size is 12, because it has 12 vertices.
   • It is planar because it's edges can be drawn in a flat plane without crossing each other. That is why Gertrude, Superperson and the Monster can fly around their Land without needing traffic lights or underpasses.
   • The diameter is 3. If Superperson can't get to where Gertrude is trying to drown the Monster, it is because she overshoots the pond by flying too far. She would never have to fly more than three ponds to get to them.
   • It is 3-regular. When Superperson and the Monster were trying to get Gertrudy to fly to all of the other ponds one by one, they flew into her pond along two of the flyways. This left Gertrude exactly one choice for flying out. This can be done from any pond because every pond has exactly three flyways touching it.

3. Tell the students that no one has ever figured out a way to draw a graph whose size is greater than 12 (a graph with more than 12 vertices) that has all of the other properties. Nor has anyone been able to figure out a good reason why it can't be done. Invite them to make mathematical history--and win a cash prize--by being the one who does it.

4. Have students experiment with this problem and try to draw the graph. If someone succeeds, send mail to MegaMath immediately!

5. When they begin working on the problem, students usually produce graphs that have most of the properties, but not quite all of them. Help students to work together and carefully check each others' graphs.

6. Have students draw large copies of graphs that almost meet the criteria and display them. This is a problem to let rest for a while and return to, off and on, for perhaps weeks. Give students plenty of time to experiment and mull it over.

   Eventually after much trial and error someone may come up with a graph that meets the criteria. Or perhaps after enough experimentation with various possibilities, someone will be able to explain why it is that size 12 is the largest that such a graph can be. If time and perseverance are what is needed to solve this problem, there is no reason why the person to solve it cannot be a child.

Ideas for Discussion

1. What strategies did you use to try and construct the graph? Where did you get stuck? What do you plan to try next?

2. Look carefully at some of the graphs mathematicians have drawn while trying to understand and solve the degree-diameter problem.

   

   

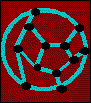
   These are the largest known graphs with the minimum degree and maximum diameter as indicated. It has been proved that the graph above with the maximum degree of 4 is the largest one that can be drawn with diameter 4, but it is not known if it is possible to draw a larger graph than the one shown that has maximum degree 3 and diameter 4.

   In general it is not known what the largest possible graphs that have relatively small degree and relatively large diameter are. Experiment with some graphs of your own and send in the graphs that you draw and what you have learned about them. Because this mathematical territory has not been studied very much, you may be the one to make a discovery that could find its way into a mathematical journal.

3. If you become convinced that it is impossible to draw a larger graph that is 3-regular, planar and has diameter 3, explain to them that "I tried for hours to do this and couldn't," is not a statement that proves that whatever they were trying to do is impossible.

4. You can show that it is impossible to make a 3-regular, planar, graph of diameter 3 that has 13 vertices. You can demonstrate that there is no sense in trying to do this because it can't be done. Here's how: (It is a Proof by Contradiction.
   • Draw the 13 vertices.
   • Make each vertex degree 3 by drawing the all three edges that will touch each vertex. Now you have 13 vertices, each with half an edge touching it.
   • In order to make the graph that we are trying to make, you will have to connect pairs of half-edges to make single whole edges. But count the number of half-edges--there are 13 x 3 = 39 of them!
   • Every time you connect two vertices together you will use up two of the half-edges. There is no way to connect the vertices together without having one half-edge left over. Therefore, you can be sure that you are wasting your time trying to make a 3-regular graph of size 13, much less one that is planar and has diameter 3.
   • What other sizes of graph are certain not to work?

What next